Recursive Formula in Maple

[Faye]

Does anyone have any idea how to write a recursive formula in Maple 11? I've already figured out how to write explicit formulas, but I can't figure out the recursive formulas. I'm probably going to fail this assignment; it is due friday.

 

[Siamese cat]

Maybe this will help:

www.math.uic.edu/~jan/mcs320/Lec16/lec16.pdf
http://www.maplesoft.com/applications/view.aspx?SID=4096&view=html

I'm more of a Matlab kind of girl, so I'm not really sure if there are any differences regarding this issue from one release of the Maple to another.

 

[Bird]

Does anyone have any idea how to write a recursive formula in Maple 11? I've already figured out how to write explicit formulas, but I can't figure out the recursive formulas. I'm probably going to fail this assignment; it is due friday.

You are not going to fail.

 

[~jet]

Does anyone have any idea how to write a recursive formula in Maple 11? I've already figured out how to write explicit formulas, but I can't figure out the recursive formulas. I'm probably going to fail this assignment; it is due friday.

Guh; I had a teacher in college who likened recursion to 'the force,' showing us a pared down version of star wars the first day of class (ever time, I had to take and drop the course several times.)

 

[enfp can be shy]

Nothing fancy, this example of a Fibonacci function from the first link that Siamese cat posted is very clear:

> fib := proc(n::nonnegint)
[LEFT]> description `returns the nth Fibonacci number`:
> if n = 0 then
> return 0:
> elif n = 1 then
> return 1:
> else
> return fib(n-2)+fib(n-1):
> end if;[/LEFT]
> end proc;

 

[NeverAmI]

I really don't know what I am doing, but I can't resist!

Does your recursive formula actually need to solve a practical purpose? If not, it shouldn't be too bad. Essentially you have two numbers to signify in a simple recursion: The number to start from and the number of iterations to perform. After that it is just the formula to use.

Let's look at one from what Siamese Cat linked to.

> restart;​

> { f(n) = f(n-1) + 9, f(0) = 7};​

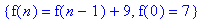
> rsolve( %, f(k));​

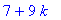
> seq( subs( k = j, %), j = 0..20);​

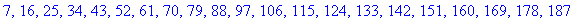
There is documentation about the rsolve command here.


In this one there are 20 iterations and the number to start from is 7, I am not sure why they are starting with 7 in this particular example.

Let's look at this line: { f(n) = f(n-1) + 9, f(0)=7};

The first comma-delimited part is the formula, the second part just defines the starting number. so the f(n) = f(n-1) is the key to the recursion in this case. All it is saying is that the current iteration is equal to the prior iteration, then you have the + 9 which means the new iteration is equal to the old iteration plus 9.

Next line is rsolve(%,f(k));

Not exactly sure what the % signifies, I am guessing it is just a callback to the previous line since that is the spot for the expression for recursion. The second part seems to be the key to iterations. From a programming standpoint, I see f(n) as an array, the f(k) which is pulling iterations from the seq command is specifying which iteration of the array is current.

seq( subs(k = j, %), j = 0..20);

the % is a callback again. From what I can gather, the subs command (substitution) is needed due to j being assigned to a sequence, so it needs a new variable in order to specify the current value.


So if you just wanted to do a simple recursion of +1 addition of whole numbers for 10 iterations starting at 0 you could use:

rsolve( { f(n) = f(n-1)+1, f(0)=0 }, f(k) );
seq(subs(k=j,%), j=0..10);

I would assume the fibonacci numbers for 10 iterations (requires 2nd order recursion) would go something like this:

rsolve( { f(n) = f(n-1)+f(n-2), f(0)=0, f(1)=1}, f(k) );
seq(subs(k=j,%), j=0..10);
​

 

[Faye]

So my problem apparently was that I was putting a 1 instead of a 2 in the "for all n from 2 to 10" for-loop after defining a[1] for the a[n]. Also, the format was much simpler than those things.

I gave up on the last part of the assignment because it wasn't worth enough points to care about and turned it in incomplete. I hope I never have to use maple ever again.

Thanks NAI for the detailed answer.

 

[Faye]

In other news: I lack basic math skills and am really having a hard time with basic algebra, which I apparently never learned.

 

[Faye]

Also: FUCK MAPLE

 

[arbygil]

If it makes you feel any better, sing the Lady Gaga song, "Paparazzi" but exchange the word "Paparazzi" with "Fibonacci."

It might not help you get a better answer, but I'll bet it'll make you groan or smile.

 

[IndigoSensor]

This thread is sickening!

 

[Faye]

I think I might have a Maple 11 lab every week for the rest of the semester. FML. Seriously, FML.

I have another one and no clue at all what to do. How the hell do you learn this program?

 

[NaeturVindur]

This thread is sickening!

what, too much code for you?

IF Answer="Yes"
     THEN
          PRINT "Why are you in this subforum?"
     ELSE
          PRINT "Why?"
ENDIF

[/nerdiness]